A Steepest Descent Method for Set Optimization Problems with Set-Valued Mappings of Finite Cardinality
Por um escritor misterioso
Last updated 12 abril 2025

9.11.20 Wen Sun, Cornell University - Video on Demand

Computer-Aided Molecular Design of Ionic Liquids as Advanced Process Media: A Review from Fundamentals to Applications

ICML 2023 Posters

An augmented Lagrangian method for optimization problems with structured geometric constraints
Performance of RIS-aided near-field localization under beams approximation from real hardware characterization, EURASIP Journal on Wireless Communications and Networking

Certifying the Absence of Spurious Local Minima at Infinity

Steepest Descent Method - an overview

The difficulty of computing stable and accurate neural networks: On the barriers of deep learning and Smale's 18th problem
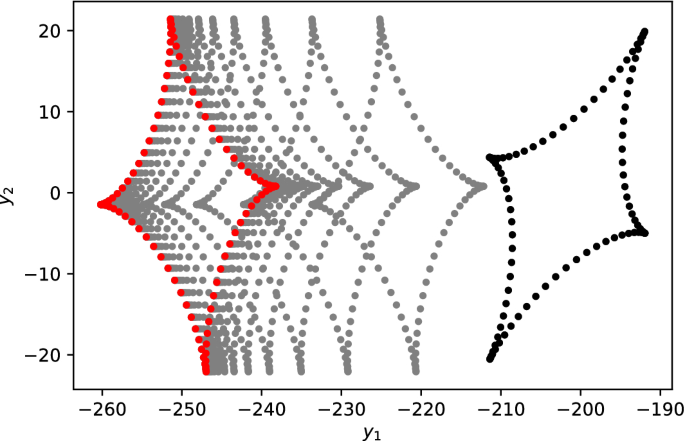
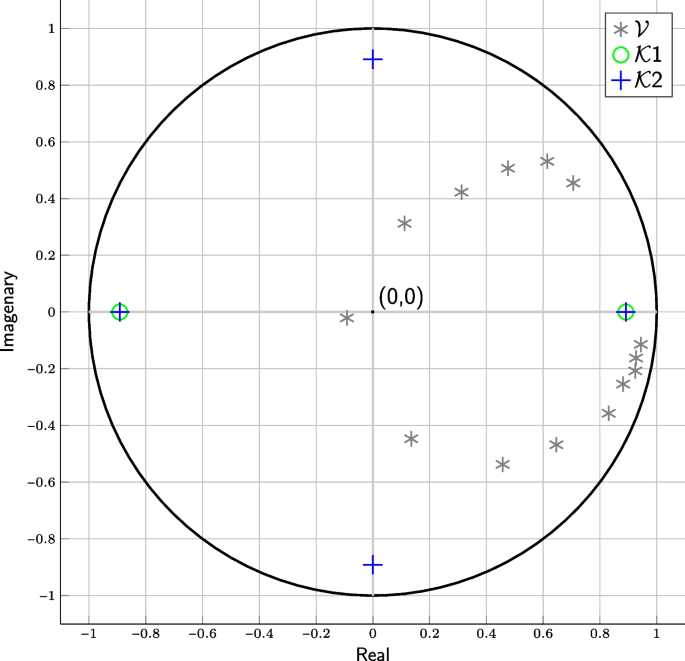
A Steepest Descent Method for Set Optimization Problems with Set-Valued Mappings of Finite Cardinality

arxiv-sanity

An adjoint‐based solver with adaptive mesh refinement for efficient design of coupled thermal‐fluid systems - Gallorini - 2023 - International Journal for Numerical Methods in Fluids - Wiley Online Library

Steepest Descent Method - an overview

An Introduction To Continuous Optimization, PDF, Mathematical Optimization
Recomendado para você
-
 On q-steepest descent method for unconstrained multiobjective optimization problems12 abril 2025
On q-steepest descent method for unconstrained multiobjective optimization problems12 abril 2025 -
 Steepest Descent and Newton's Method in Python, from Scratch: A Comparison, by Nicolo Cosimo Albanese12 abril 2025
Steepest Descent and Newton's Method in Python, from Scratch: A Comparison, by Nicolo Cosimo Albanese12 abril 2025 -
 matrices - How is the preconditioned conjugate gradient algorithm related to the steepest descent method? - Mathematics Stack Exchange12 abril 2025
matrices - How is the preconditioned conjugate gradient algorithm related to the steepest descent method? - Mathematics Stack Exchange12 abril 2025 -
 The A-Z Guide to Gradient Descent Algorithm and Its Types12 abril 2025
The A-Z Guide to Gradient Descent Algorithm and Its Types12 abril 2025 -
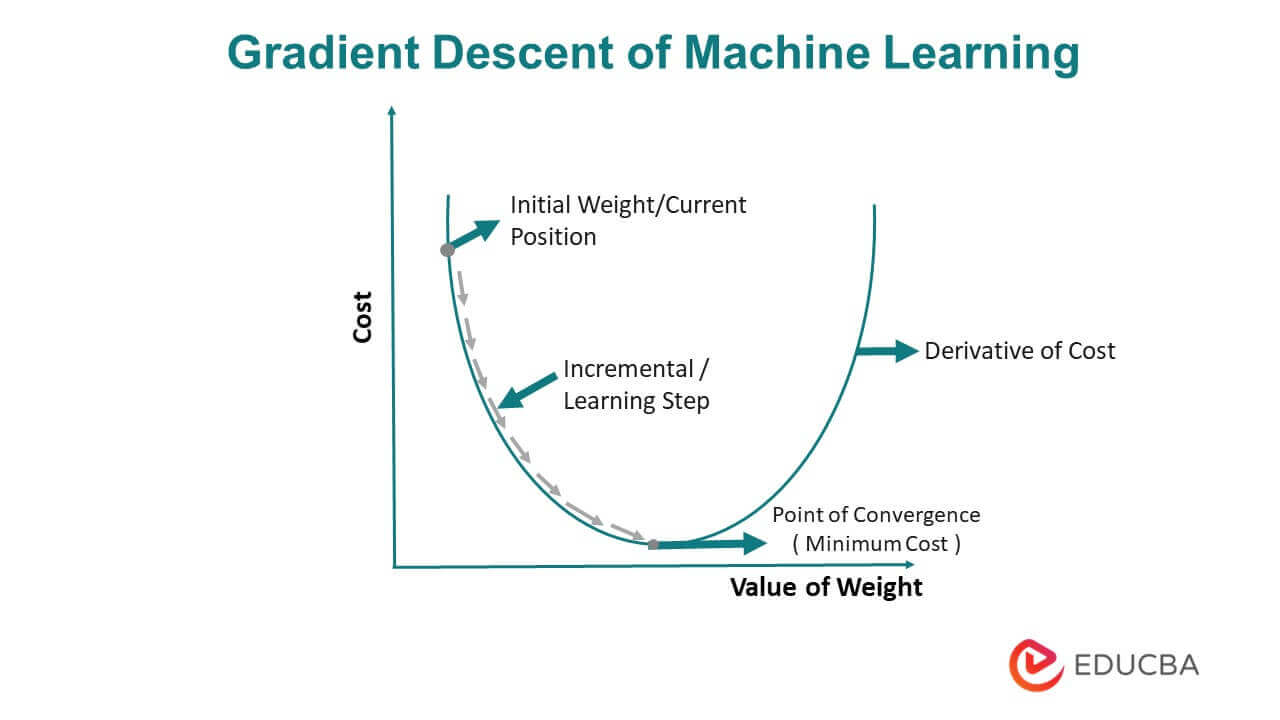 Gradient Descent in Machine Learning: Optimized Algorithm12 abril 2025
Gradient Descent in Machine Learning: Optimized Algorithm12 abril 2025 -
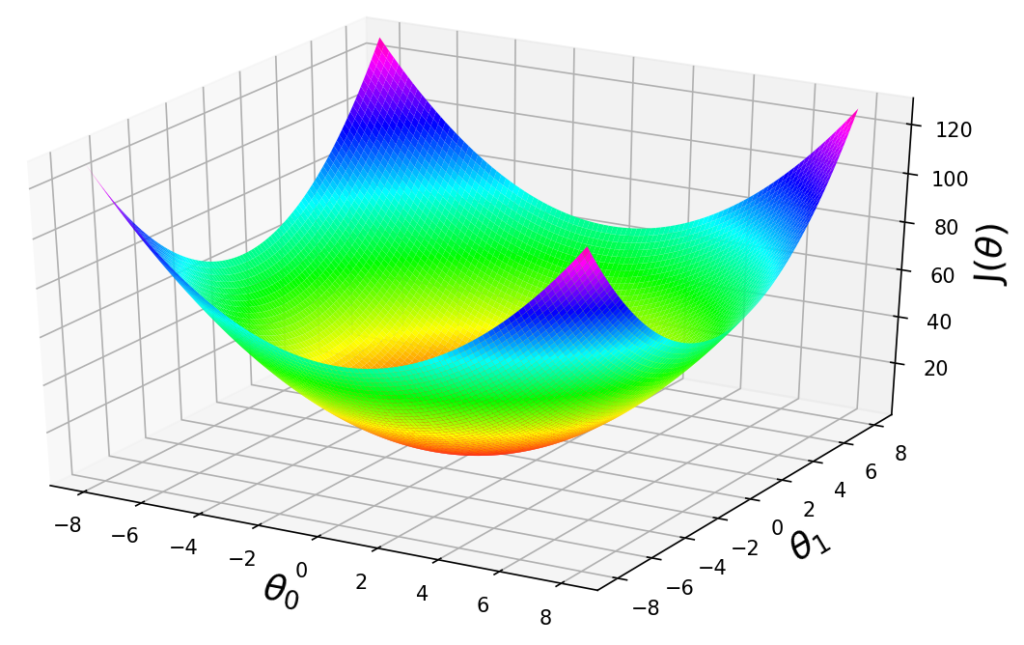 Guide to Gradient Descent Algorithm: A Comprehensive implementation in Python - Machine Learning Space12 abril 2025
Guide to Gradient Descent Algorithm: A Comprehensive implementation in Python - Machine Learning Space12 abril 2025 -
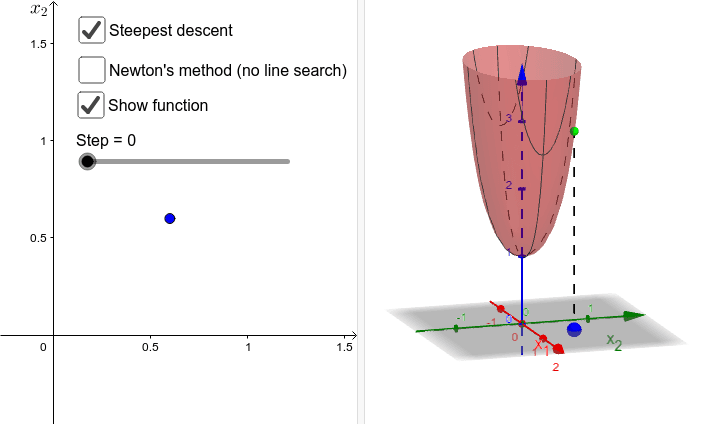 Steepest descent vs gradient method – GeoGebra12 abril 2025
Steepest descent vs gradient method – GeoGebra12 abril 2025 -
MathType - The #Gradient descent is an iterative optimization #algorithm for finding local minimums of multivariate functions. At each step, the algorithm moves in the inverse direction of the gradient, consequently reducing12 abril 2025
-
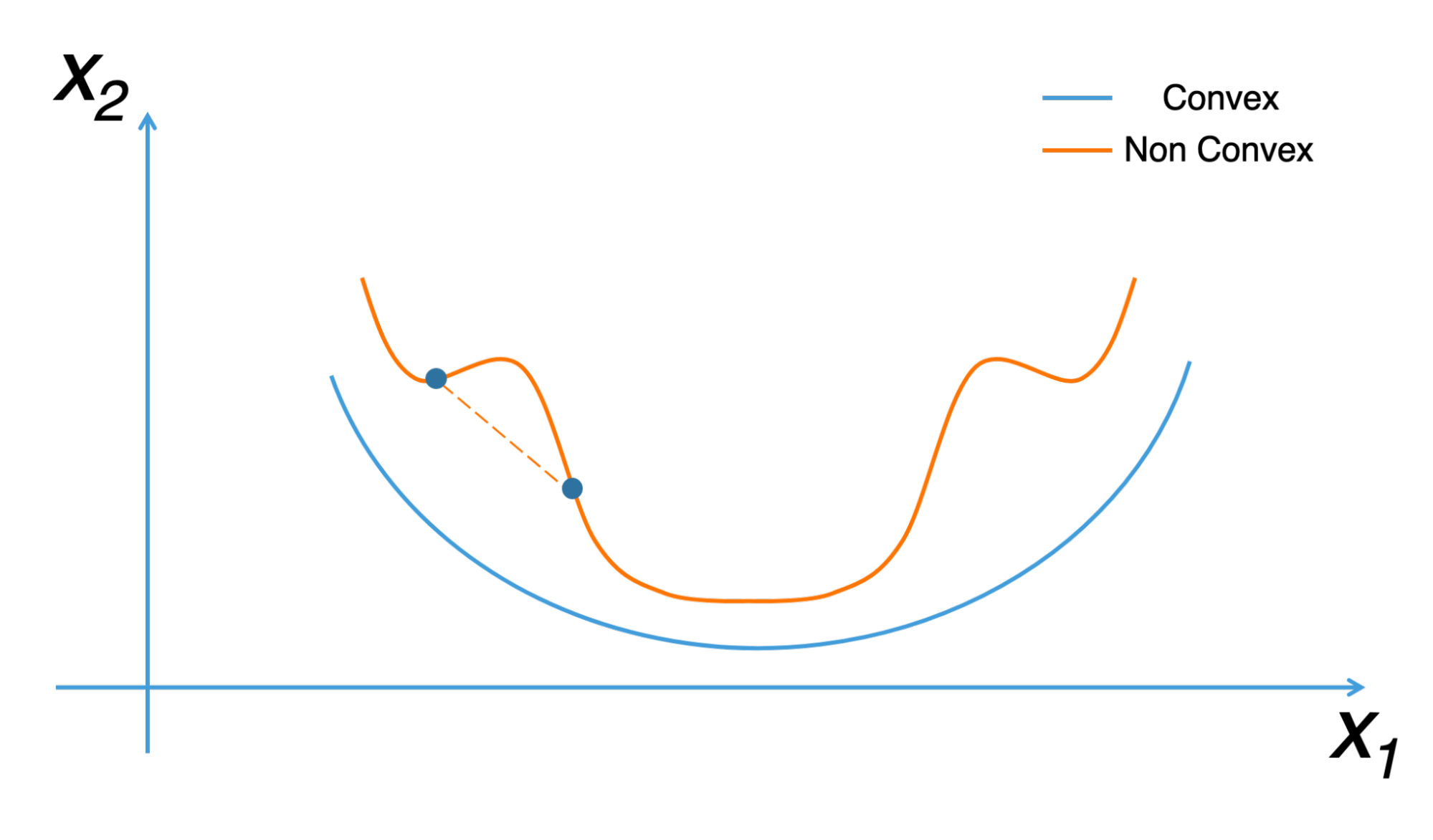 Gradient Descent Tutorial12 abril 2025
Gradient Descent Tutorial12 abril 2025 -
 Stochastic Gradient Descent Algorithm With Python and NumPy – Real Python12 abril 2025
Stochastic Gradient Descent Algorithm With Python and NumPy – Real Python12 abril 2025
você pode gostar
-
 Governo inaugura reforma da Secretaria de Planejamento - - Notícias do Acre12 abril 2025
Governo inaugura reforma da Secretaria de Planejamento - - Notícias do Acre12 abril 2025 -
 Gif-cr7 by facuedicionestv on DeviantArt12 abril 2025
Gif-cr7 by facuedicionestv on DeviantArt12 abril 2025 -
 Sonic Chaos Announcement Trailer (fan game)12 abril 2025
Sonic Chaos Announcement Trailer (fan game)12 abril 2025 -
![Fix Roblox Windows 10 Edition Won't Install or Download - [Tutorial]](https://i.ytimg.com/vi/mx0Q72jEjwU/hq720.jpg?sqp=-oaymwEhCK4FEIIDSFryq4qpAxMIARUAAAAAGAElAADIQj0AgKJD&rs=AOn4CLDlaIBZQle4URB14QM3E0I1XJbshw) Fix Roblox Windows 10 Edition Won't Install or Download - [Tutorial]12 abril 2025
Fix Roblox Windows 10 Edition Won't Install or Download - [Tutorial]12 abril 2025 -
![Nissan S14 Drift [Add-On / FiveM]](https://img.gta5-mods.com/q75/images/nissan-s14-drift-fivem-addon/91bb1c-Screenshot_14.jpg) Nissan S14 Drift [Add-On / FiveM]12 abril 2025
Nissan S14 Drift [Add-On / FiveM]12 abril 2025 -
 ♡ : r/traumacore12 abril 2025
♡ : r/traumacore12 abril 2025 -
 Syphon Filter 2 - Playstation 1 – Retro Raven Games12 abril 2025
Syphon Filter 2 - Playstation 1 – Retro Raven Games12 abril 2025 -
 Roupas - Branco - Tamanho 4GG - Freestyle12 abril 2025
Roupas - Branco - Tamanho 4GG - Freestyle12 abril 2025 -
 Desenho de Moto de trilha para colorir - Tudodesenhos12 abril 2025
Desenho de Moto de trilha para colorir - Tudodesenhos12 abril 2025 -
 What if SCP-999 Wore SCP-035?12 abril 2025
What if SCP-999 Wore SCP-035?12 abril 2025
