Rooks Problem -- from Wolfram MathWorld
Por um escritor misterioso
Last updated 04 abril 2025

The rook is a chess piece that may move any number of spaces either horizontally or vertically per move. The maximum number of nonattacking rooks that may be placed on an n×n chessboard is n. This arrangement is achieved by placing the rooks along the diagonal (Madachy 1979). The total number of ways of placing n nonattacking rooks on an n×n board is n! (Madachy 1979, p. 47). In general, the polynomial R_(mn)(x)=sum_(k)r_k^((m,n))x^k whose coefficients r_k^((m,n)) give the

The Philosophy Program at LaGuardia Community College
Mathematica on the cheap [ David Antler ]
In how many ways can you arrange eight queens on a standard chessboard in such a way that none of them is attacking any other? - Quora

Rook Complement Graph -- from Wolfram MathWorld
Yet Another Math Programming Consultant: More queens problems

Solved Let B be the 8 by 8 chessboard with forbidden cells

How 8 Queens Works

Rook Number -- from Wolfram MathWorld

Rook Polynomial -- from Wolfram MathWorld
IGraph/M Documentation

Using Boolean Computation to Solve Some Problems from Ramsey Theory « The Mathematica Journal
Recomendado para você
-
Setting Up Pieces on ChessUp - ChessUp Knowledge Base04 abril 2025
-
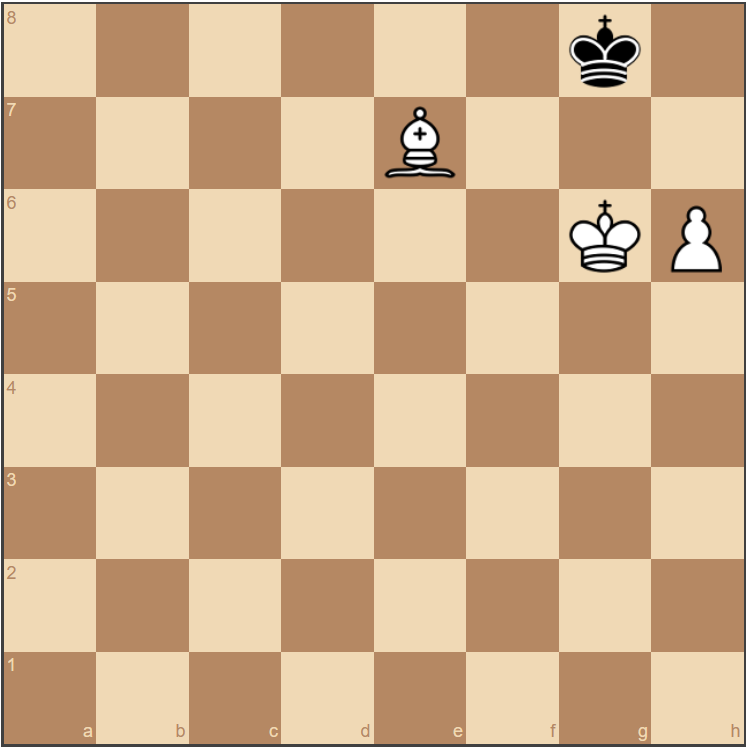 Complete Guide To Chess Endgames04 abril 2025
Complete Guide To Chess Endgames04 abril 2025 -
Yet Another Math Programming Consultant: Chess and solution pool04 abril 2025
-
 Problem - 1342E - Codeforces04 abril 2025
Problem - 1342E - Codeforces04 abril 2025 -
Polinomios de Rook, PDF, Mathematics04 abril 2025
-
 Rook Polynomials: A Straight-Forward Problem – Feature Column04 abril 2025
Rook Polynomials: A Straight-Forward Problem – Feature Column04 abril 2025 -
 CHAPTER 4 OTHER FORKS/DOUBLE ATTACKS Diagram 124 - White wins a Rook or Knight in 2 moves.04 abril 2025
CHAPTER 4 OTHER FORKS/DOUBLE ATTACKS Diagram 124 - White wins a Rook or Knight in 2 moves.04 abril 2025 -
 Radicaln Marble Chess Set 15 Inches Black & Multi Green Handmade Chess Board Game - 1 Chess Board & 32 Chess Pieces - 2 Player Games for Adults - Chess Sets Game : Toys & Games04 abril 2025
Radicaln Marble Chess Set 15 Inches Black & Multi Green Handmade Chess Board Game - 1 Chess Board & 32 Chess Pieces - 2 Player Games for Adults - Chess Sets Game : Toys & Games04 abril 2025 -
 Why Rooks Worth More than Bishops?04 abril 2025
Why Rooks Worth More than Bishops?04 abril 2025 -
A queen is a queen but nothing trumps a pair of lionhearted rooks in either strength or majesty sweeping across an open board! This…04 abril 2025
você pode gostar
-
![Asterisk War Part 1 [Blu-ray] [2018] : Movies & TV](https://m.media-amazon.com/images/W/MEDIAX_792452-T2/images/I/61bpuxyHciL._AC_UF894,1000_QL80_.jpg) Asterisk War Part 1 [Blu-ray] [2018] : Movies & TV04 abril 2025
Asterisk War Part 1 [Blu-ray] [2018] : Movies & TV04 abril 2025 -
 Mahjong Connect 3 - Mahjong Games Free04 abril 2025
Mahjong Connect 3 - Mahjong Games Free04 abril 2025 -
 Star Wars Bestiario - Mejores Criaturas y Alienígenas de la Saga04 abril 2025
Star Wars Bestiario - Mejores Criaturas y Alienígenas de la Saga04 abril 2025 -
Daniel Cesar Clínica Cirúrgica - Ooforoplastia é uma cirurgia ovariana realizada para retirar cistos ou nódulos do ovário, sem retirar o órgão por inteiro. É uma técnica que preserva o ovário possibilitando (04 abril 2025
-
 História Novata da Akatsuki - Obrigado Senpai - História escrita por Hyuululu - Spirit Fanfics e Histórias04 abril 2025
História Novata da Akatsuki - Obrigado Senpai - História escrita por Hyuululu - Spirit Fanfics e Histórias04 abril 2025 -
 The Smurfs - Wikipedia04 abril 2025
The Smurfs - Wikipedia04 abril 2025 -
 BOTW recipes posters Botw zelda, Geek food, Zelda breath of wild04 abril 2025
BOTW recipes posters Botw zelda, Geek food, Zelda breath of wild04 abril 2025 -
 Your Love is a Lie Music Video - Simple Plan Image (7259817) - Fanpop04 abril 2025
Your Love is a Lie Music Video - Simple Plan Image (7259817) - Fanpop04 abril 2025 -
 Here's How to Get the Bold Eyebrows of Your Dreams04 abril 2025
Here's How to Get the Bold Eyebrows of Your Dreams04 abril 2025 -
 Juni Taisen Stage Play's Visual Reveals Entire Cast in Costume - News - Anime News Network04 abril 2025
Juni Taisen Stage Play's Visual Reveals Entire Cast in Costume - News - Anime News Network04 abril 2025


