1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Por um escritor misterioso
Last updated 10 abril 2025


Day 18 Warm-Up 1) Which of the following problems is a circle and which is a parabola? Why? A) ppt download
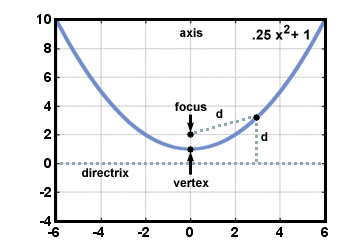
Conic Sections Parabolas Summary & Analysis

Write a polar equation of a conic with the focus at the orig

Find the vertex, focus, and directrix of the parabola, and s

Solved 1. Use the definition of the parabola to write an
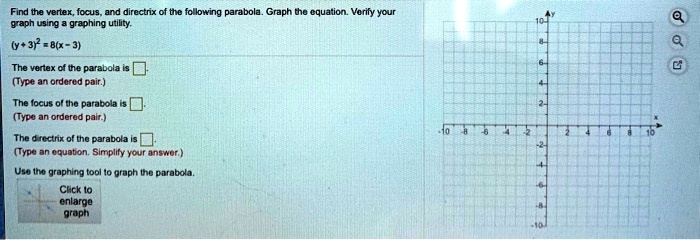
SOLVED: Find the vertex, focus, and directrix of the following parabola. Graph the equation using a graphing tool. (y + 3)^2 = 8(x - 2) The vertex of the parabola is (2,


Find a polar equation of the conic with its focus at the pole. Parabola; (8, 0)

Saddle point - Wikipedia
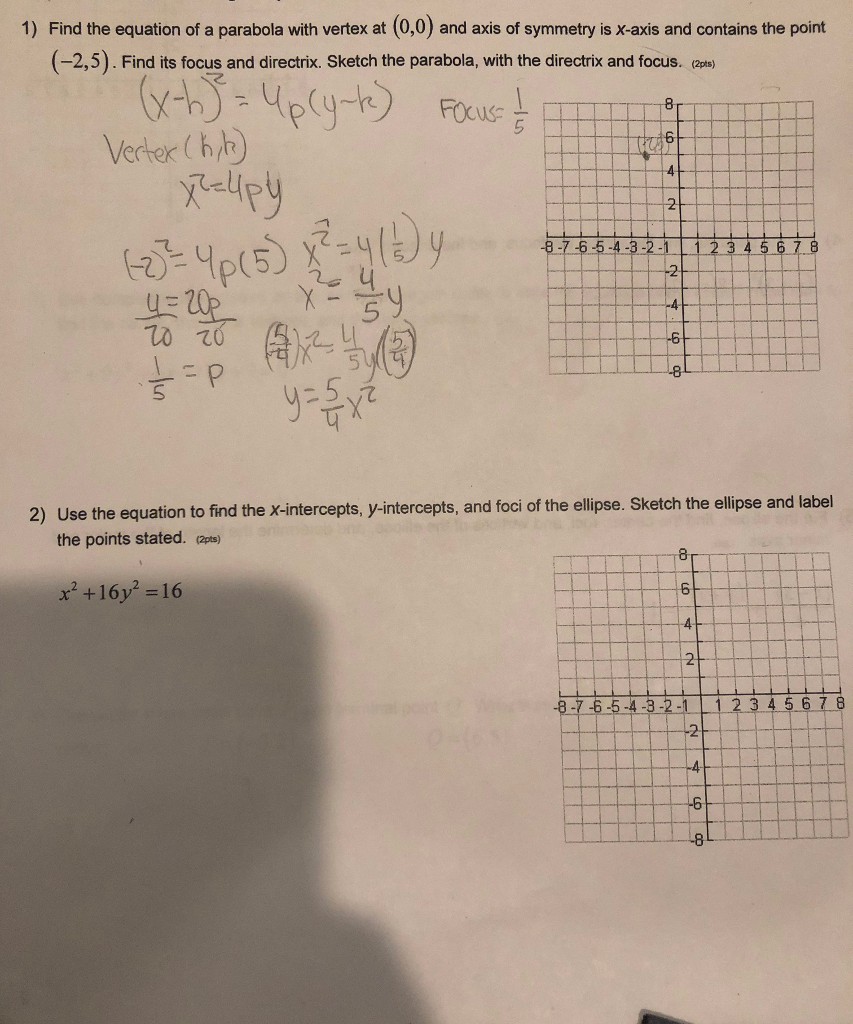
Solved Find the equation of a parabola with vertex at (0,0)

Day 18 Warm-Up 1) Which of the following problems is a circle and which is a parabola? Why? A) ppt download
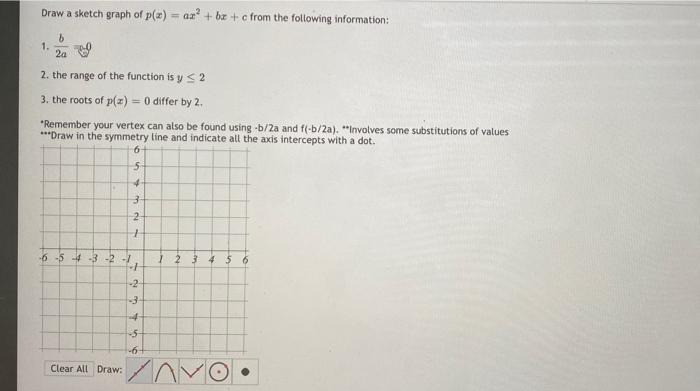
Solved Find the equation for the parabola that has its focus

Conic sections: Analyzing Conic Sections with the Algebraic Method - FasterCapital

Conic sections: Analyzing Conic Sections with the Algebraic Method - FasterCapital

Solved Chapter 10 1) Find the equation of the parabola with
Recomendado para você
-
 DirectX 12 - Download for PC Free10 abril 2025
DirectX 12 - Download for PC Free10 abril 2025 -
 Learning DirectX 12 – Lesson 1 – Initialize DirectX 1210 abril 2025
Learning DirectX 12 – Lesson 1 – Initialize DirectX 1210 abril 2025 -
 Fortnite Chapter 4 - DirectX 11 vs DirectX 12 vs Performance Mode - FPS Boost10 abril 2025
Fortnite Chapter 4 - DirectX 11 vs DirectX 12 vs Performance Mode - FPS Boost10 abril 2025 -
 TiledLighting11 DirectX® 11 SDK Sample - AMD GPUOpen10 abril 2025
TiledLighting11 DirectX® 11 SDK Sample - AMD GPUOpen10 abril 2025 -
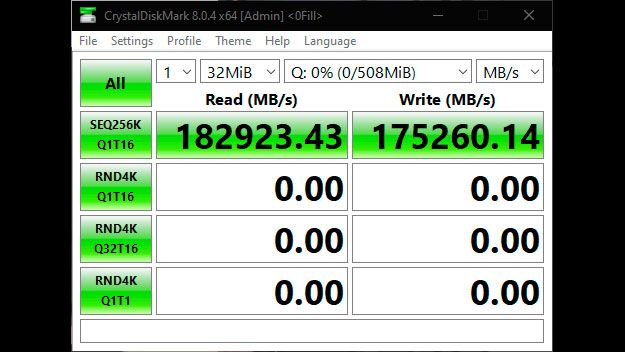 AMD 3D V-Cache enables RAM disk to hit 182 GB/s speeds — over 12X faster than the fastest PCIe 5.0 SSDs10 abril 2025
AMD 3D V-Cache enables RAM disk to hit 182 GB/s speeds — over 12X faster than the fastest PCIe 5.0 SSDs10 abril 2025 -
 CrossOver announces DirectX 12 support coming to macOS10 abril 2025
CrossOver announces DirectX 12 support coming to macOS10 abril 2025 -
![Square Enix Unveils Impressive WITCH CHAPTER 0 [cry] DirectX 12 Tech Demo At Microsoft BUILD](https://imageio.forbes.com/blogs-images/marcochiappetta/files/2015/04/witch-cry-2.jpg?height=400&width=711&fit=bounds) Square Enix Unveils Impressive WITCH CHAPTER 0 [cry] DirectX 12 Tech Demo At Microsoft BUILD10 abril 2025
Square Enix Unveils Impressive WITCH CHAPTER 0 [cry] DirectX 12 Tech Demo At Microsoft BUILD10 abril 2025 -
 Dungeon Lords review10 abril 2025
Dungeon Lords review10 abril 2025 -
 Introduction to 3D Game Programming with DirectX 1210 abril 2025
Introduction to 3D Game Programming with DirectX 1210 abril 2025 -
 Should you have DirectX 12 shaders downloaded if you use performance mode? : r/FortniteCompetitive10 abril 2025
Should you have DirectX 12 shaders downloaded if you use performance mode? : r/FortniteCompetitive10 abril 2025
você pode gostar
-
 Golden Short Chainsaw Man Denji Cosplay Wig Heatresistant Synthetic Halloween Costume ▻ ▻ Free Shipping ▻ Up to 70% OFF10 abril 2025
Golden Short Chainsaw Man Denji Cosplay Wig Heatresistant Synthetic Halloween Costume ▻ ▻ Free Shipping ▻ Up to 70% OFF10 abril 2025 -
asdasdasdas10 abril 2025
-
Genius Quiz10 abril 2025
-
 Swapped Shapes & Beats, Wiki10 abril 2025
Swapped Shapes & Beats, Wiki10 abril 2025 -
 Sobre Grade Saveiro Cross 2017 a 2023 Aço Inox Cromado Elite10 abril 2025
Sobre Grade Saveiro Cross 2017 a 2023 Aço Inox Cromado Elite10 abril 2025 -
 Danmachi volume 16 Freya Dungeon ni deai, Relationship images, Fantasy world10 abril 2025
Danmachi volume 16 Freya Dungeon ni deai, Relationship images, Fantasy world10 abril 2025 -
 GM Supi(white) vs Magnus. Mate in 3, white to move : r/chess10 abril 2025
GM Supi(white) vs Magnus. Mate in 3, white to move : r/chess10 abril 2025 -
 Microsoft investigates Outlook.com bug breaking email search10 abril 2025
Microsoft investigates Outlook.com bug breaking email search10 abril 2025 -
 Kimetsu no Yaiba Temporada 3: cuándo, cómo y a qué hora ver el estreno del Arco de la Villa de los Herreros10 abril 2025
Kimetsu no Yaiba Temporada 3: cuándo, cómo y a qué hora ver el estreno del Arco de la Villa de los Herreros10 abril 2025 -
 Download Transparent Tuxedo T - Imagenes De Ropa En Roblox PNG Image with No Backgroud - PNGkey.com10 abril 2025
Download Transparent Tuxedo T - Imagenes De Ropa En Roblox PNG Image with No Backgroud - PNGkey.com10 abril 2025
