Solved Prove that for a matrix with entries in F[λ] (or
Por um escritor misterioso
Last updated 04 abril 2025
![Solved Prove that for a matrix with entries in F[λ] (or](https://media.cheggcdn.com/media/d73/d73e2bc6-667d-4f65-9048-ad140647fb3d/phpR0SFVN)
Answer to Solved Prove that for a matrix with entries in F[λ] (or
![Solved Prove that for a matrix with entries in F[λ] (or](https://www.frontiersin.org/files/Articles/1055071/fams-08-1055071-HTML-r1/image_m/fams-08-1055071-g001.jpg)
Frontiers Numerical analysis of finite difference schemes arising from time-memory partial integro-differential equations
![Solved Prove that for a matrix with entries in F[λ] (or](https://ars.els-cdn.com/content/image/3-s2.0-B9780323917209000218-f17-06-9780323917209.gif)
Hessian Matrix - an overview
![Solved Prove that for a matrix with entries in F[λ] (or](https://wikimedia.org/api/rest_v1/media/math/render/svg/93ae9a358221f8217accfeafbb4be81cefb39e64)
Cayley–Hamilton theorem - Wikipedia
![Solved Prove that for a matrix with entries in F[λ] (or](https://media.cheggcdn.com/media/826/826a3530-065e-4859-a31d-edd68a3a44fd/phpJg68Hz.png)
Solved 2. (a) Let A, B E Mmxn (F). Prove that rank(A + B) <
![Solved Prove that for a matrix with entries in F[λ] (or](https://www.statlect.com/images/normal-matrix__11.png)
Normal matrix
![Solved Prove that for a matrix with entries in F[λ] (or](https://docs.sympy.org/latest/_downloads/a2eb0f47e21015de38f03325bc45d081/matrices-6.hires.png)
Matrices (linear algebra) - SymPy 1.12 documentation
![Solved Prove that for a matrix with entries in F[λ] (or](https://glmnet.stanford.edu/articles/glmnet_files/figure-html/unnamed-chunk-6-1.png)
An Introduction to `glmnet` • glmnet
![Solved Prove that for a matrix with entries in F[λ] (or](https://waynemystir.github.io/assets/axler-ch07-exer-B-15.png)
Linear Algebra Done Right Ch.7 Exercises
![Solved Prove that for a matrix with entries in F[λ] (or](https://i.ytimg.com/vi/l_JhNtB0D0M/maxresdefault.jpg)
Show that λ is an eigenvalue of A and find a corresponding eigenvector
![Solved Prove that for a matrix with entries in F[λ] (or](https://d2nchlq0f2u6vy.cloudfront.net/20/11/04/59f5f92cbec71e0ba798a1a140e40fab/866b7714f418bd89f72fd655cf047307/lateximg_large.png)
Prove: If λ is an eigenvalue of an invertible matrix A and x
![Solved Prove that for a matrix with entries in F[λ] (or](https://cdn.numerade.com/ask_images/e96865e177cd4ba3a9f597eff03063c1.jpg)
SOLVED: Please answer the following by completing the steps in MATLAB. When you are finished, please copy the entire command window that you used for each question and paste it into a
![Solved Prove that for a matrix with entries in F[λ] (or](https://wikimedia.org/api/rest_v1/media/math/render/svg/63e497ef48780c585f7fe176e7c61d508ae0eb60)
Condition number - Wikipedia
![Solved Prove that for a matrix with entries in F[λ] (or](https://content.bartleby.com/qna-images/question/55da46bf-d110-4b1f-8323-6e5068c15bea/d32f81a7-89e6-4692-b838-3cfa3386b015/c38cgko_processed.jpeg)
Answered: For an invertible matrix A, prove that…
![Solved Prove that for a matrix with entries in F[λ] (or](https://yutsumura.com/wp-content/uploads/2016/11/eigenvalue-eigenvector-eye-catch-1024x512.jpg)
Eigenvalues of a Matrix and its Transpose are the Same
![Solved Prove that for a matrix with entries in F[λ] (or](https://pubs.acs.org/cms/10.1021/acs.jpclett.1c01885/asset/images/acs.jpclett.1c01885.social.jpeg_v03)
Structure Determination of Europium Complexes in Solution Using Crystal-Field Splitting of the Narrow f–f Emission Lines
Recomendado para você
-
 Caseiforme - Dicio, Dicionário Online de Português04 abril 2025
Caseiforme - Dicio, Dicionário Online de Português04 abril 2025 -
 Inigualável: Pelé se torna verbete do dicionário - BAHIA NO AR04 abril 2025
Inigualável: Pelé se torna verbete do dicionário - BAHIA NO AR04 abril 2025 -
 Biblioteca Brasiliana Guita e José Mindlin04 abril 2025
Biblioteca Brasiliana Guita e José Mindlin04 abril 2025 -
 Copy - Plumwood Mountain04 abril 2025
Copy - Plumwood Mountain04 abril 2025 -
 tinôco on X: gnt acho que não entendi a trend kkkk Defina brega em apenas uma imagem: / X04 abril 2025
tinôco on X: gnt acho que não entendi a trend kkkk Defina brega em apenas uma imagem: / X04 abril 2025 -
 Oficial! Pelé é eternizado em dicionário 'Aquele que é fora do comum' - The News 2 - News at your Doorstep04 abril 2025
Oficial! Pelé é eternizado em dicionário 'Aquele que é fora do comum' - The News 2 - News at your Doorstep04 abril 2025 -
 WRS-TTS0000-1 | SEN M-TO-1/1-TO-1 F/C EUR; WIRELESS ROOM TEMP SENSOR SETPOINT ADJ SCALE: 13 TO 29 DEGREES C OR 55 TO | Johnson Controls04 abril 2025
WRS-TTS0000-1 | SEN M-TO-1/1-TO-1 F/C EUR; WIRELESS ROOM TEMP SENSOR SETPOINT ADJ SCALE: 13 TO 29 DEGREES C OR 55 TO | Johnson Controls04 abril 2025 -
 The Canon text and manuscripts of the New Testament.. . V4 . x ., . EtLpaucatAcvjuLSfj t>^;-*Xx<r*T»e &b *v? c o 71 cd ess^ &©*£/a> p of£ fi& TW £/ tonat^M, uevr^y, £•04 abril 2025
The Canon text and manuscripts of the New Testament.. . V4 . x ., . EtLpaucatAcvjuLSfj t>^;-*Xx<r*T»e &b *v? c o 71 cd ess^ &©*£/a> p of£ fi& TW £/ tonat^M, uevr^y, £•04 abril 2025 -
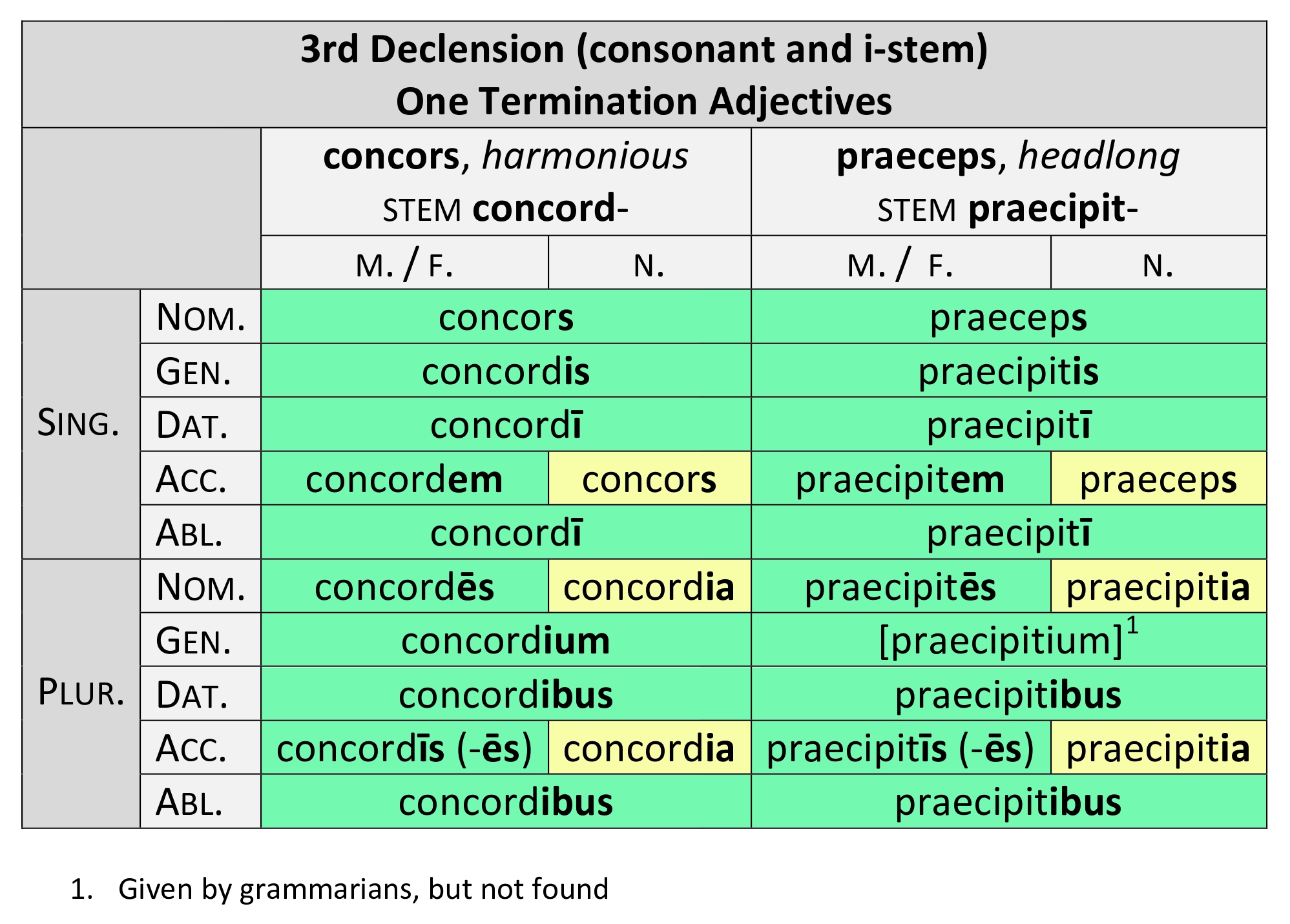 3rd Decl. (Cons. and i-stem) Adj., 1 Termination (2 of 4)04 abril 2025
3rd Decl. (Cons. and i-stem) Adj., 1 Termination (2 of 4)04 abril 2025 -
 Blueprint reading; a practical manual of instruction in blueprint reading through the analysis of typical plates with reference to mechanical drawing conventions and methods, the laws of projection, etc . Ii ;:,:v;i04 abril 2025
Blueprint reading; a practical manual of instruction in blueprint reading through the analysis of typical plates with reference to mechanical drawing conventions and methods, the laws of projection, etc . Ii ;:,:v;i04 abril 2025
você pode gostar
-
 Cachorro : Desenhos para colorir, Desenhos para crianças, Jogos04 abril 2025
Cachorro : Desenhos para colorir, Desenhos para crianças, Jogos04 abril 2025 -
 Nintendo Releases Official Zelda Breath Of The Wild Recap Video04 abril 2025
Nintendo Releases Official Zelda Breath Of The Wild Recap Video04 abril 2025 -
 Rihanna RUSSIAN ROULETTE Drawing by Anshu Kaulitz - Fine Art America04 abril 2025
Rihanna RUSSIAN ROULETTE Drawing by Anshu Kaulitz - Fine Art America04 abril 2025 -
 Aid for Ukrainian Refugees in Romania Rotary Camena Piatra Neamt04 abril 2025
Aid for Ukrainian Refugees in Romania Rotary Camena Piatra Neamt04 abril 2025 -
 Café artesanal da família Ximenes chega aos EUA04 abril 2025
Café artesanal da família Ximenes chega aos EUA04 abril 2025 -
 Zombies 3: Trailer, Cast, Plot Release Date04 abril 2025
Zombies 3: Trailer, Cast, Plot Release Date04 abril 2025 -
 Mirai Nikki – OVA, Simple Edition, DVD04 abril 2025
Mirai Nikki – OVA, Simple Edition, DVD04 abril 2025 -
 Resident Evil: The Final Chapter Resident Evil: The Final Chapter Wesker (Shawn Roberts) Movie Costumes original movie costume04 abril 2025
Resident Evil: The Final Chapter Resident Evil: The Final Chapter Wesker (Shawn Roberts) Movie Costumes original movie costume04 abril 2025 -
 Sixtus IV appointing Bartolomeo Platina to the prefectury of the Acrylic Print by Roberto Morgenthaler - Pixels04 abril 2025
Sixtus IV appointing Bartolomeo Platina to the prefectury of the Acrylic Print by Roberto Morgenthaler - Pixels04 abril 2025 -
Idle Burger Empire Tycoon—Game Ver. 1.1.6 MOD APK Unlimited Money - - Android & iOS MODs, Mobile Games & Apps04 abril 2025